因果推断导论笔记-Lecture10-Causal Graphical Models-Average Causal Effect
检验马氏相容性
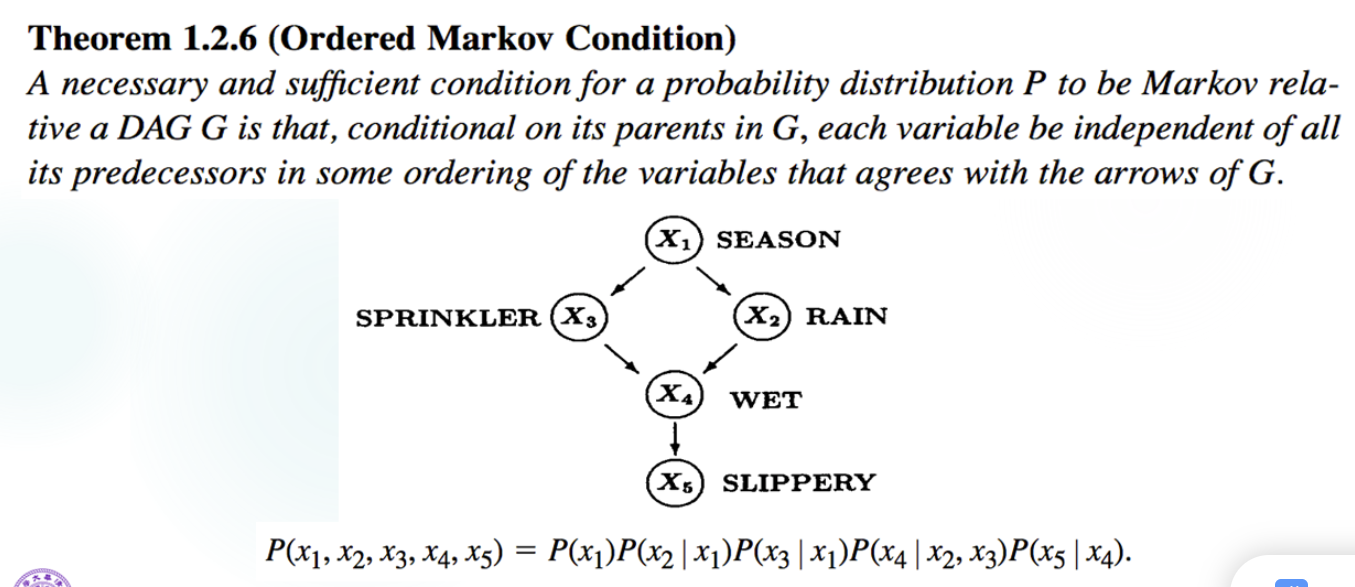

图模型的问题
从概率到图:

从上面可以看出,马氏相容性只是限制了I(G)不会太多,但可能太少。
从图到概率:

增加新的假设,忠实性假设:

等价图的定义:
相同骨架和V结构,就在等价类里面。

注意不是相同的V结构数目,也就是点是不动的。
找到一个有向无环图,意味着找到了因果的含义吗?
不是。
因果体现了数据的生成机制,例如真正的因果是X -> Y,但画起图来是X->Y和X<-Y是等价类。
也就是说现在的图模型只是概率与图的关系,而不是因果与图的关系。
因果贝叶斯网络
引入干预:intervention,度量因果作用

干预的影响:
- 被干预的变量,扔掉影响它的边(即没有父节点)
- 其他变量的父节点不变
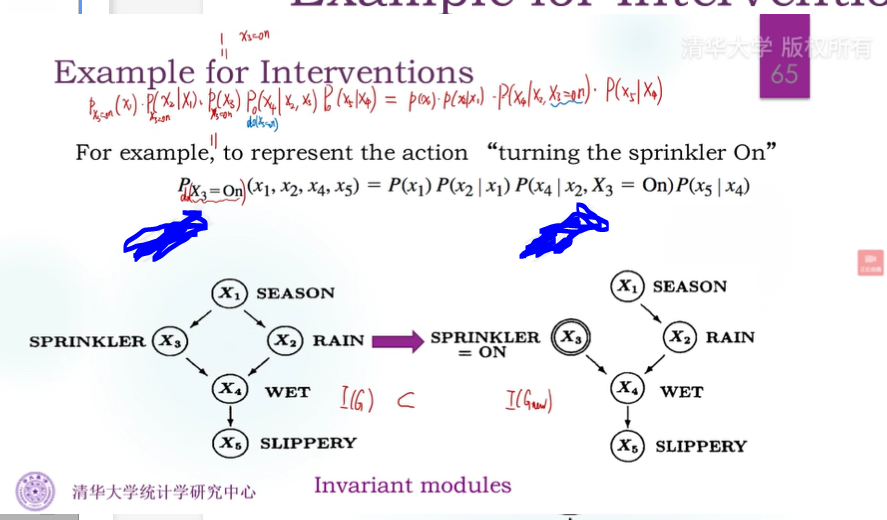
注意和的含义是不同的,后者是现实世界的条件概率。


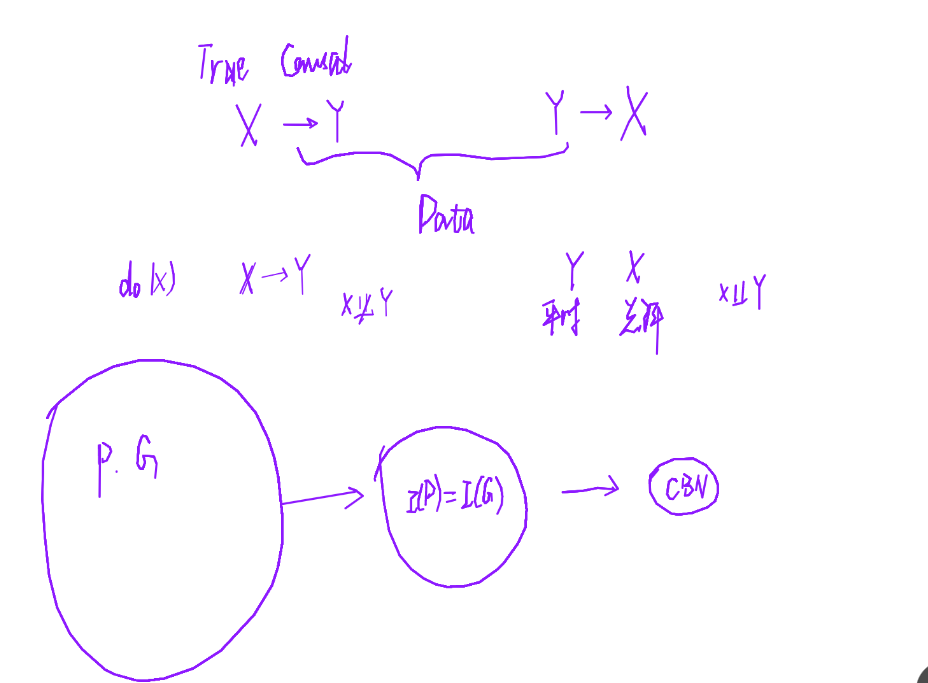
干预后,就可以区分上面两种等价图了。
和Rubin框架的比较:
- 干预和潜在结果是类似的;反事实也类似于
- Rubin框架从数据到概率更清晰明确
其他模型
结构方程模型
把原因放在右侧,结果放在左侧,本身不包含因果作用。

通过这个模型理解三个层次:

-
关联性
P(Y | H=2)
-
干预的层级(类似superpopulation)
-
反事实的层级(类似sub sample)
专注在某位同学上,观测误差是给定的了,在想象的这个层级里,降低了随机性。
Observation for Joe:X=0.5, H=1, Y=1.5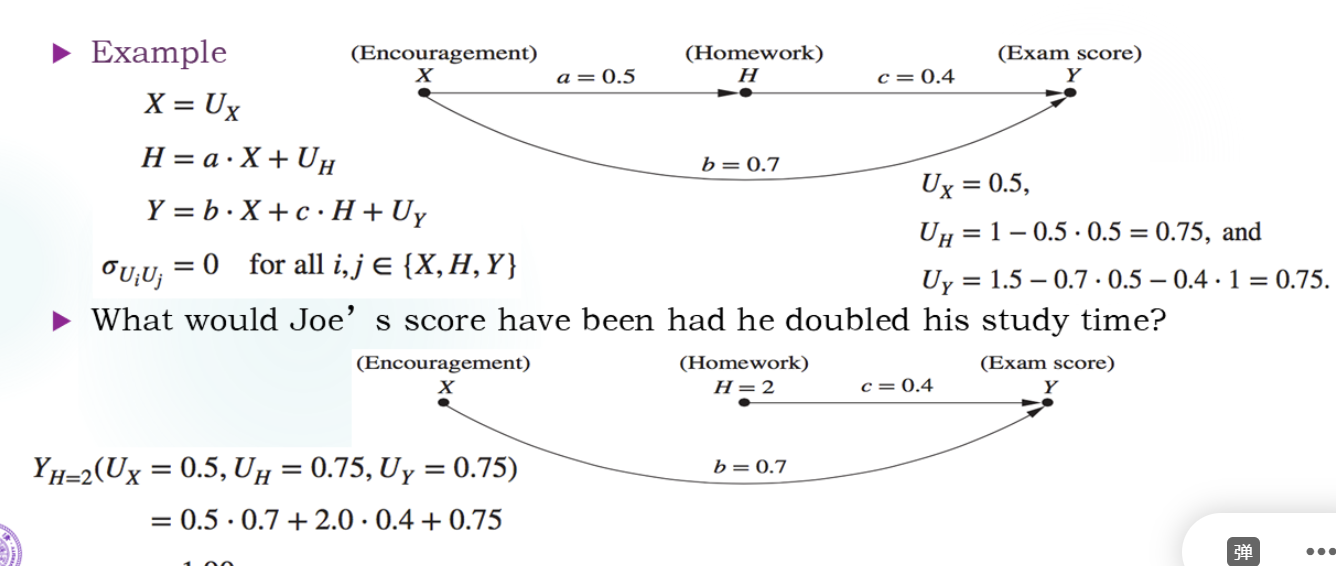
ACE under Known Causal Structure
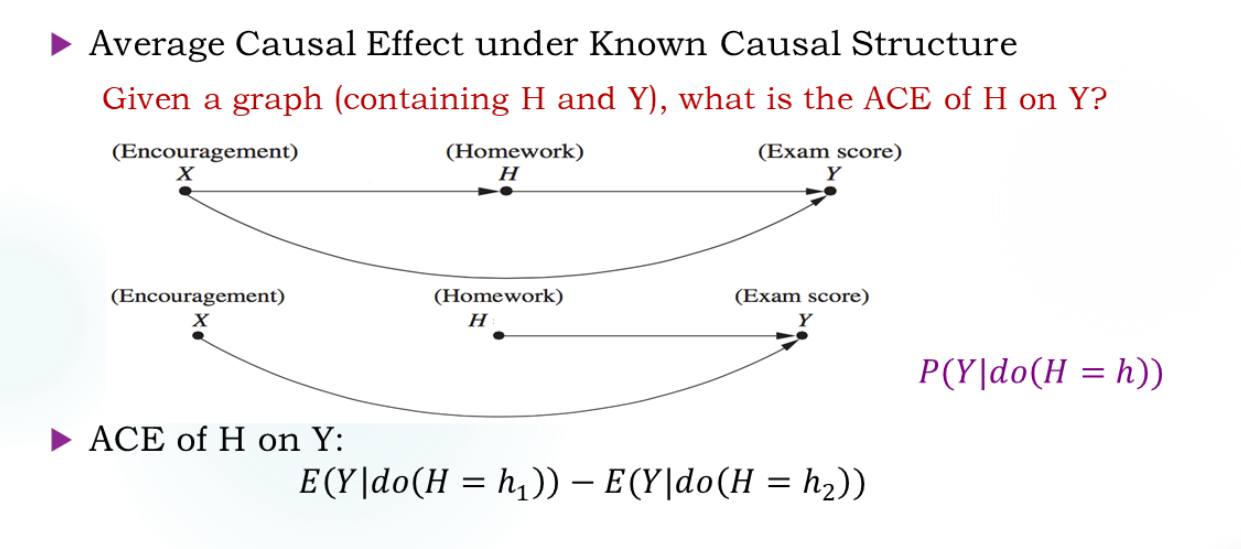
重点是如何搭建观测数据和干预世界的关系:





因果推断导论笔记-Lecture10-Causal Graphical Models-Average Causal Effect
https://bebr2.com/2022/11/28/因果推断导论笔记-Lecture10-Causal Graphical Models-Average Causal Effect/